在研究柏拉圖問題關於「期望值」這件事情時，有想到一件事情，但是並沒有去多想，但是還是講一下好了...
了解一下常態分佈（我知道大大們一定都會了，當做複習吧XD）

常態分佈(高斯分佈)：將一連續變項之觀察值發生機率以圖呈現其分布情形，且具有以下特性：
1.以平均數為中線，構成左右對稱之單峰、鐘型曲線分布。
2.觀察值之範圍為負無限大至正無限大之間。
3.變項之平均數、中位數和眾數為同一數值。
標準差 (standard deviation)：

68.3%的數值，落在平均數±1個標準差間；
95.4%的數值，落在平均數±2個標準差間；
99.7%的數值，落在平均數±3個標準差間。

我們在之前的舉例中有提到:"將所有100顆球分為100種不同的價值為1,2,3,...,100。接下來..."
這樣的話適合利用在最一開始的研究「了解並研究柏拉圖的解」上，但是如果搬到凋謝速率和期望值上來的話就會不一樣了...以凋謝速率做例子好了：

假如現在第1,2,3,4的店家價值各是3,7,11,5，如果是像以前的作法會像是這樣：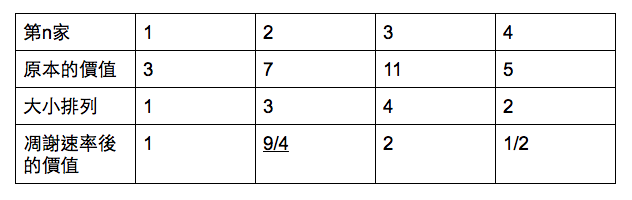
會發現，如果用大小排列的話，會發現第二家店的價值是最大(9/4)的。
再來看如果不排列直接將凋謝速率乘上去會發生怎麼樣的情形：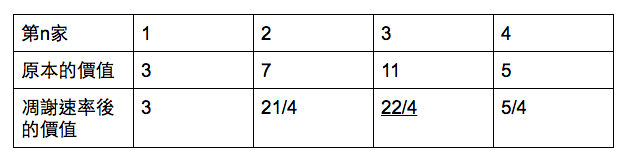

結果第三家是最大的。

討論：
之前的東西在加上凋謝速率後就不一樣了，因為如果有差異太大的兩朵花，直接乘是大的贏，但是如果是有加上比例限制的話，小的反而有可能會贏，所以這樣的指定會影響到選擇...
雖然大小會影響到結果，但是我想還是先以大小為基準，先不考慮數值的不平均性。說真的到底如果要用數值的話，還要考慮到常態分佈吧...
轉換成「期望值」的部分就更難處理了，因為要想我所說的期望值到底是「第幾大」還是「分數在全部的多少」去討論了。

不知道有沒有人懂我的意思？